Generowanie terenu 3D
Uogólnienie przypadku generowania losowego terenu w 2D

Jakiś czas temu pisałem o jednym ze sposobów generowania dwuwymiarowego, losowego terenu. Nie zagłębiając się w liczne możliwe zastosowania pokazałem jak przy pomocy języka JavaScript wygenerować odpowiednie obrazki i umieścić je na stronie. Cały wpis można zobaczyć tutaj: Generowanie losowego terenu 2D. Wspomniałem też o możliwości rozszerzenia algorytmu na trzeci wymiar i możliwe sposoby implementacji ewentualnego generatora. Napisałem też, że być może wkrótce do tego tematu wrócę. Jak powiedziałem, tak też zamierzam teraz zrobić. Żeby nie zajmować czasu tym, dla których efekt nie jest tym, czego szukają, przedstawię najpierw wynik działania skryptu:
Zachęcam do pobawienia się różnymi przełącznikami i suwakami. Każdy z nich ma swoje przeznaczenie. Żeby nie zabijać starszych komputerów ustawiłem dość niski poziom szczegółów (obliczenia wymagane są głównie przy definiowaniu oświetlenia poszczególnych bloków). Sam algorytm generowania terenu jest bardzo sprawny, co można zaobserwować zaznaczając opcję siatki. Co więcej, generowanie ukształtowania terenu jest najczęściej operacją jednorazową. Można ją wykonać raz, dane zapisać w pamięci i szybko do nich sięgać jeżeli zajdzie taka potrzeba.
Algorytm wyznaczania ukształtowania terenu
Metoda wbrew pozorom nie jest skomplikowana. Wszystko polega na losowym przesuwaniu środka kwadratu. Popatrzmy na ilustrację:
Wyliczenia zaczynamy od czterech punktów krańcowych. Mogą one być wygenerowane losowo, ale mogą być również ustawione według jakiegoś innego algorytmu, a nawet ustawione na 0. W pierwszej kolejności wyliczany jest punkt środkowy liczony jako średnia czterech krańcowych pomniejszona lub powiększona o losową wartość. Gdy wartość ta jest duża, teren jest mocno pofałdowany, gdy jest mała, teren jest gładki. W szczególności, gdy losowe przesunięcie wynosi 0, otrzymujemy płaską mapę. Drugim krokiem jest wyliczenie trzech lub czterech innych środków. Zauważmy, że po wyliczeniu punktu Z możemy utworzyć cztery kwadraty zbudowane kolejno z punktów:
- A-Z-B-X,
- B-Z-C-X,
- C-Z-D-X,
- D-Z-A-X.
Punkt X jest tutaj wirtualny, ale łatwo sobie wyobrazić, gdzie on na tym obrazku powinien się znaleźć dla każdego z kwadratów. Jeżeli punkt X wykracza poza mapę, liczymy średnią z trzech punktów. Są jednak inne przypadki, w których punkt jest znany, ale o tym za chwilę. Przypuśćmy, że wyliczyliśmy średnią wysokości kwadratu A-Z-B-X, dodaliśmy losowe przesunięcie Δ1 i nazwaliśmy ten punkt B, wyliczyliśmy też środek kwadratu D-Z-A-X, dodaliśmy losowe przesunięcie Δ2 i nazwaliśmy ten punkt D, punkt Z nazwaliśmy C. Te nowe punkty pokazane zostały na poniższej ilustracji:
Jak łatwo zauważyć, znów otrzymujemy, nazwijmy to sobie w ten sposób, poziomy kwadrat. Taki sam, z jakim mieliśmy do czynienia w pierwszym kroku operacji. Nie trzeba już chyba mówić, że całą operację można wykonywać wielokrotnie, aż do uzyskania pożądanego rozmiaru mapy lub dokładności. Warto też zauważyć, że średnia z trzech punktów liczona jest tylko na zewnętrznych krawędziach całej mapy. Kwadrat A-B-C-D wyznaczany w większości punktami koloru zielonego nie ma górnej krawędzi i nie ma krawędzi lewej, podobnie jak kwadrat wyjściowy. Punkt X dla podkwadratu prawego może być jednak wyznaczony w poprzednim kroku iteracji, bo przecież obok też jest zwykły kwadrat, taki sam, również mający określony środek.
Zmniejszanie przesunięcia środka
Jasne jest, że Δ, losowe przesunięcie środka nie może być jednakowe dla każdego z kwadratów. Rozsądne wydaje się zastosowanie proporcjonalnie większego przesunięcia dla dużych kwadratów i mniejszego dla podkwadratów. Naturalnym stosunkiem wydaje się tutaj stosunek 2 - 2 razy większy kwadrat to dwa razy większe przesunięcie Δ. Nie jest to jednak sztywna reguła. Dzielenie przesunięcia w każdym kroku przez wartość większą niż 2 (lub mnożenie przez współczynnik mniejszy niż 0,5) pozwala osiągnąć bardziej gładkie wykończenia. Dzielenie przesunięcia w każdym kroku przez wartość mniejszą niż 2 (lub mnożenie przez współczynnik większy niż 0,5) pozwala osiągnąć bardziej chropowate wykończenia. To, jaki efekt chcemy uzyskać zależy tylko od nas. Lekkie pagórki lub zielone wzgórza są gładkie, ale już dzikie szczyty gór skalistych bardziej poszarpane.
Wyliczanie oświetlenia terenu
W wielu przypadkach sam proces generowania ukształtowania terenu jest wystarczający do osiągnięcia zamierzonych celów. Postanowiłem jednak pójść o krok dalej i upiększyć nieco powstający teren. Wiele języków programowania nadaje się do tego znacznie lepiej niż JavaScript, wiele bibliotek do tworzenia trójwymiarowych przestrzeni korzystających ze sprzętowego wspomagania obliczeń może to zrobić znacznie szybciej, biblioteki OpenGL oraz DirectX w zasadzie tych wyliczeń nawet nie wymagają. Ze względu na miejsce umieszczenia algorytmu, stronę internetową i przyjęty język obsługiwany przez przeglądarki, JavaScript, postanowiłem to zrobić właśnie w tym języku. Jedną z podstawowych czynności przy tworzeniu aplikacji jest dobór odpowiednich narzędzi. Moim zdaniem strony internetowe nie wyposażone w żadne dodatkowe, zewnętrzne komponenty (wtyczki Flash, Silverlight, Unity), interfejsy bez pełnego wsparcia różnych przeglądarek (WebGL). Być może zdanie to, pisane w 2014 roku, straci ważność. Póki co, trójwymiarowa grafika w JavaScript to raczej ciekawostka niż rywal wymienionych wcześniej komponentów i interfejsów.
Jak wyliczyć poziom oświetlenia powierzchni? Zrozumiałe jest, że słońce świeci mocniej tam, gdzie kąt padania na powierzchnię jest równy kątowi prostemu. Im ten kąt bardziej odbiega od idealnego, tym naświetlenie, czyli jasność, jest mniejsze. W szczególności, gdy promienie słoneczne są równoległe do powierzchni, naświetlenie jest zerowe. Nie rozważam przypadków, gdy powierzchnia jest odwrócona. W praktyce nawet nieoświetlone powierzchnie nie są idealnie czarne. Wpływ na to ma światło odbite i rozproszone, czy to przez chmury czy to przez inne obiekty.
Należy zatem wyliczyć kąty nachylenia każdej z powierzchni wygenerowanego terenu. W siatce terenu minimalnym obiektem składowym były czworokąty wyznaczane przez cztery punkty. Jest taka zasada matematyczna, że w przestrzeni trójwymiarowej płaszczyznę definiuje się na podstawie trzech punktów. Cztery punkty nie muszą wcale leżeć na jednej płaszczyźnie i najczęściej nie leżą (leżą tylko w szczególnych przypadkach, zakładając, że są to cztery różne punkty). Nasze czworokąty należy zatem przekroić na pół i stworzyć z nich dwa trójkąty o wspólnej przekątnej. Otrzymamy wtedy dwie jednoznacznie określone powierzchnie. Takie trójkąty są już łatwe w dalszej analizie.
Zamiast liczyć kąt pomiędzy promieniami światła a płaszczyzną zmienię trochę sposób patrzenia - na bardziej matematyczny, równoważny. Obliczę kąt pomiędzy wektorem normalnym powierzchni (trójkąta) a wektorem hipotetycznego słońca. Wektor normalny do powierzchni liczony jest jako iloczyn wektorowy dwóch wektorów tworzonych z punktów trójkąta. Tak, wiem, za dużo różnych pojęć, za dużo wektorów. Spróbuję to nieco rozwikłać.
Trójkąt to trzy punkty: P1, P2 i P3. Wektor reprezentujący bok trójkąta A = [P1, P2] oblicza się ze wzoru:
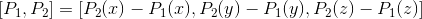
Podobnie wyliczamy wektor B = [P2, P3]. Te dwa wektory to boki trójkąta. Jeżeli chcemy teraz wyznaczyć wektor prostopadły do płaszczyzny reprezentowanej przez parę wektorów [A, B], możemy się posłużyć iloczynem wektorowym:
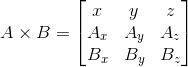
Przekształcając odpowiednio wyrażenie otrzymujemy co następuje:
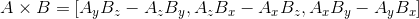
Jeżeli kierunek wektorów jest zgodny z ruchem wskazówek zegara, wektor styczny zwrócony jest w kierunku powierzchni, jeżeli wektory kierują się przeciwnie, wektor ma zwrot przeciwny. Teraz można skorzystać z kolejnej matematycznej zależności - iloczyn skalarny wektorów jest równy długości tych wektorów pomnożonej przez cosinus kąta pomiędzy nimi. Wyraża się to wzorem:
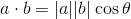
Wystarczy teraz już tylko zdefiniować wektor słońca i dla każdego z trójkątów obrazka wyliczyć wektor normalny i jego kąt względem słońca. Im większe oświetlenie tym jaśniejszy zielony odcień.
Przykładowa implementacja
Po wstępie teoretycznym czas na jakiś fragment kodu. Kod został celowo rozbity na wiele bloków w celu pokazania kolejnych kroków wyliczania wysokości terenu w poszczególnych miejscach, oddzielnie liczone są wektory i oświetlenie. Sam widok 3D sprowadzony został do widoku izometrycznego. Oto kod:
<html> <head> <title>3DTerrain</title> <link href="bootstrap.min.css" rel="stylesheet" /> </head> <body> <canvas class="img-responsive" id="terrainCanvas" width="700" height="400"></canvas> <div> <div class="form-group"> <label>Szczegóły<input id="detailLevel" type="range" min="0" max="5" /></label> </div> <div class="form-group"> <label>Wypiętrzenie<input id="upthrustLevel" type="range" min="0.5" max="1.2" step="0.1" value="0.9" /></label> </div> <div class="form-group"> <label><input id="drawGrid" type="checkbox" /> Siatka</label> </div> <button class="btn btn-default" id="generate" onclick="generateTerrain()">Generuj</button> </div> <script> (function () { var rand = function (range) { return Math.random() * 2 * range - range; }, //2 wektory w postaci tablic [x,y,z], ułożone przeciwnie do ruchu wskazówek zegara normal = function (v1, v2) { var v = new vector( v1[1] * v2[2] - v1[2] * v2[1], v1[2] * v2[0] - v1[0] * v2[2], v1[0] * v2[1] - v1[1] * v2[0]); v.normalize(); return v; }, vector = function (x, y, z) { var self = this; self.x = x; self.y = y; self.z = z; self.length = Math.sqrt(x * x + y * y + z * z); //Normalizacja wektora, sprowadzenie jego długości do 1 self.normalize = function () { self.x /= self.length; self.y /= self.length; self.z /= self.length; self.length = 1; }; self.dot = function (v) { return self.x * v.x + self.y * v.y + self.z * v.z; } }, //wektor słońca sunVector = (function () { var v = new vector(-1, 1, -2); v.normalize(); return v; })(), sun = function (v) { //światło padające na płaszczyznę return -v.dot(sunVector); }, fill = function (array, size, range, suppr) { var arr = array, SIZE = size, osc = Math.sqrt(suppr); while (size > 1) { var r = size / 2; range *= osc; for (var y = r; y <= SIZE; y += size) for (var x = r; x <= SIZE; x += size) arr[x][y] = rand(range) + (arr[x - r][y - r] + arr[x - r][y + r] + arr[x + r][y - r] + arr[x + r][y + r]) / 4; range *= osc; for (var y = 0; y <= SIZE; y += size) for (var x = r; x <= SIZE; x += size) arr[x][y] = rand(range) + (arr[x - r][y] + arr[x + r][y] + (arr[x][y - r] || 0) + (arr[x][y + r] || 0)) / (y < r || y + r > SIZE ? 3 : 4); for (var y = r; y <= SIZE; y += size) for (var x = 0; x <= SIZE; x += size) arr[x][y] = rand(range) + ((arr[x - r] ? arr[x - r][y] : 0) + (arr[x + r] ? arr[x + r][y] : 0) + arr[x][y - r] + arr[x][y + r]) / (x < r || x + r > SIZE ? 3 : 4); size /= 2; } }; generateTerrain = function () { var g = terrainCanvas.getContext("2d"), toHex2 = function (x) { return x < 16 ? "0" : x.toString(16); }, toColor = function (v) { var g = Math.round(80 + 100 * v); //Obliczenie natężenia składowej zielonej return "#00" + toHex2(g) + "00"; }, DETAILS = +detailLevel.value,//0-5 MAP_SIZE = 3 + DETAILS, ARR_SIZE = Math.pow(2, MAP_SIZE) + 1, tileDiff = +upthrustLevel.value, initialDiff = tileDiff * Math.pow(2, MAP_SIZE - 1), initialSuppression = 0.5, sx = 20, ts = Math.pow(2, 5 - DETAILS) * 0.6, tsx = Math.pow(2, 5 - DETAILS) * 1.25, tsy = Math.pow(2, 5 - DETAILS) * 0.6, sy = 200, terrain = new Array(ARR_SIZE); for (var i = 0; i < ARR_SIZE; i++) terrain[i] = new Array(ARR_SIZE); terrain[0][0] = 0;//rand(initialDiff); terrain[0][ARR_SIZE - 1] = 0;//rand(initialDiff); terrain[ARR_SIZE - 1][0] = 0;//rand(initialDiff); terrain[ARR_SIZE - 1][ARR_SIZE - 1] = 0;//rand(initialDiff); fill(terrain, ARR_SIZE - 1, initialDiff, initialSuppression); g.clearRect(0, 0, terrainCanvas.width, terrainCanvas.height); if (drawGrid.checked) { //Draw grid g.strokeStyle = "#000"; for (var x = 0; x < ARR_SIZE; x++) { g.beginPath(); g.moveTo(sx + x * tsx, sy + x * tsy - terrain[x][0] * ts); for (var y = 1; y < ARR_SIZE; y++) { g.lineTo(sx + (x + y) * tsx,sy + (x - y) * tsy - terrain[x][y] * ts); } g.stroke(); g.closePath(); } for (var y = 0; y < ARR_SIZE; y++) { g.beginPath(); g.moveTo(sx + y * tsx, sy - y * tsy - terrain[0][y] * ts); for (var x = 1; x < ARR_SIZE; x++) { g.lineTo(sx + (x + y) * tsx, sy + (x - y) * tsy - terrain[x][y] * ts); } g.stroke(); g.closePath(); } } else { for (var y = 0; y < ARR_SIZE - 1; y++) for (var x = 0; x < ARR_SIZE - 1; x++) { var v = normal( [0, -1, terrain[x][y] - terrain[x][y + 1]], [1, 0, terrain[x + 1][y] - terrain[x][y]]); g.beginPath(); g.moveTo(sx + (x + 1 + y) * tsx, sy + (x + 1 - y) * tsy - terrain[x + 1][y] * ts); g.lineTo(sx + (x + y) * tsx, sy + (x - y) * tsy - terrain[x][y] * ts); g.lineTo(sx + (x + y + 1) * tsx, sy + (x - y - 1) * tsy - terrain[x][y + 1] * ts); g.fillStyle = toColor(sun(v)); g.strokeStyle = toColor(sun(v)); g.closePath(); g.fill(); g.stroke(); v = normal( [0, 1, terrain[x + 1][y + 1] - terrain[x + 1][y]], [-1, 0, terrain[x][y + 1] - terrain[x + 1][y + 1]]); g.beginPath(); g.moveTo(sx + (x + y + 1) * tsx, sy + (x - y - 1) * tsy - terrain[x][y + 1] * ts); g.lineTo(sx + (x + y + 2) * tsx, sy + (x - y) * tsy - terrain[x + 1][y + 1] * ts); g.lineTo(sx + (x + y + 1) * tsx, sy + (x - y + 1) * tsy - terrain[x + 1][y] * ts); g.fillStyle = toColor(sun(v)); g.strokeStyle = toColor(sun(v)); g.closePath(); g.fill(); g.stroke(); } } } window.addEventListener("load", generateTerrain); })(); </script> </body> </html>
Fragment można sobie skopiować lokalnie i przetestować z różnymi ustawieniami, nawet takimi, które nie zostały uwzględnione w interfejsie użytkownika.
Dalsze kroki
Istnieje wiele możliwości poprawienia jakości generowanych map. Można się pokusić o lepsze cieniowanie (cieniowanie Gourauda), można dostosować kolorystykę w taki sposób, aby tereny leżące wyżej niż zadany punkt przyjmowały kolor śniegu. Ładnie reprezentuje to wysokie szczyty. Można pójść w drugą stronę i tereny leżące poniżej pewnej wartości progowej wyrównać i narysować kolorem niebieskim reprezentującym morze lub inny akwen. Można teren upstrzyć drzewkami i inną roślinnością ozdobną. Dla zaawansowanych polecam wprowadzenie jeszcze jednej techniki wpływającej na kształt terenu i bardzo ładnie reprezentującej naturę. Technika polega na wybraniu kilku, kilkunastu punktów i takie wyżłobienie terenu, jakby płynęła tamtędy rzeka. Rzeka płynie tam, gdzie jest niżej żłobiąc (obniżając teren) tym bardziej, im szybciej płynie i im więcej wody przetacza.
Zacząłem od generowania terenów 2D i powiedziałem, że może kiedyś uda się coś napisać o mapach 3D. Znów użyję podobnej formułki: jak będzie czas, możliwości, nie przerzucę się na inne zagadnienia to kto wie - być może uda się ten temat jeszcze bardziej rozwinąć.
Kategoria:JavaScriptCanvas
Brak komentarzy - bądź pierwszy