Rozkład normalny (Gaussa) w SQL Server

Czołówka rozkładów prawdopodobieństwa

Majster poucza budowlańców:
- Słuchajcie, jutro przyjeżdża komisja odbiorcza. Cokolwiek by się nie działo, udawajcie, że tak miało być.
Następnego dnia komisja ogląda budynek, a tu nagle łup - jedna ze ścian wali się z hukiem. Inspektorzy odskakują przerażeni, a stojący obok robotnik spokojnie spoglądając na zegarek oznajmia:
- No tak, 10.43. Wszystko zgodnie z harmonogramem.

Rozkład normalny, nazywany, pewnie nawet częściej, rozkładem Gaussa, jest jednym z najważniejszych rozkładów prawdopodobieństwa. Okazuje się, że wiele naturalnie występujących zjawisk w przyrodzie i procesów przemysłowych da się w przybliżeniu wyrazić krzywą Gaussa. Nic więc dziwnego, że stosuje się tę krzywą oraz cały, powiązany z tą krzywą, mocno rozbudowany, aparat analityczny w statystyce. Takie analizy mogą się przydać również w SQL. Powiem więcej - przed zaprojektowaniem niektórych tabel i relacji przeprowadza się testy wydajnościowe. Ten etap testów określa dalszy sposób postępowania: czy stosujemy tradycyjne, relacyjne podejście, czy też stosujemy denormalizację i struktury pomocnicze. Wiadomo nie od dziś, że SQL Server dobierając plany wykonania również opiera się na statystycznym rozkładzie wartości - są przecież statystyki, jest też pojęcie selektywności bardzo blisko związanej ze statystykami. Między innymi dlatego generując losowe i testowe dane, warto je wygenerować dobrze. W sposób zbliżony do ich naturalnego, rzeczywistego rozkładu.

Wzór funkcji

Do problemu generowania danych można podejść na kilka sposobów. Ja postanowiłem wyjść od funkcji gęstości prawdopodobieństwa. Dla mniej wtajemniczonych powiem, że wyliczając prawdopodobieństwo wystąpienia wartości z przedziału stosuje się zwykłą całkę (najczęściej w sposób numeryczny, dyskretny). Funkcja gęstości jest też chyba najczęściej kojarzona z funkcją Gaussa, bo przyjmuje charakterystyczny, dzwonopodobny kształt. Jej wzór można przedstawić następująco:

y=e^{-(x-μ)²/(2*σ²)}/_{(σ * SQRT(2*PI))}

Przerobienie tego na wersję SQL nie powinno być szczególnie trudne:

CREATE FUNCTION Gauss(@sigma float, @mi float, @x float)
RETURNS float AS
BEGIN
RETURN EXP(-(@x-@mi)*(@x-@mi)/(2*@sigma*@sigma))/(@sigma*SQRT(2*PI()));
END

Nie ma oczywiście wymogu umieszczania tych wyliczeń w oddzielnej funkcji, ale takie rozwiązanie znacząco zwiększy czytelność rozwiązania.

Po utworzeniu funkcji można już wygenerować wartości dla wskazanego przedziału.

Generowanie wartości funkcji w zadanym przedziale

Aby zwiększyć czytelność rozwiązania zastosowałem podejście wieloetapowe. Oprócz przeniesienia wyliczeń do funkcji, przeniosłem generowanie poszczególnych wartości do wyrażeń CTE. Mamy zatem kolejno:

zdefiniowanie cyfr od 0-9,
uzyskanie poprzez iloczyn kartezjański pożądanego zbioru liczb całkowitych [0, 99],
przekształcenie liniowego zbioru [0, 99] w inny liniowy [-5.0, 4.9],
wyliczenie wartości funkcji Gaussa dla zbioru [-5.0, 4.9].

Przekładając to na język T-SQL otrzymamy następujące rozwiązanie:

DECLARE @sigma float = 1;
DECLARE @mi float = 0;

WITH T10 AS --Liczby 0-9
(
  SELECT N FROM (VALUES (0), (1), (2), (3), (4), (5), (6), (7), (8), (9)) T(N)
),
T100 AS --Liczby 0-99
(
  SELECT X.N*10+Y.N N FROM T10 X
  CROSS JOIN T10 Y
),
CustomRange AS --Liczby z zakresu -5.0-4.9
(
  SELECT (N-50.0)/10.0 X FROM T100
)
SELECT X, CAST(dbo.Gauss(@sigma, @mi, X) AS decimal(9,4)) Y FROM CustomRange

Zmienne @sigma oraz @mi decydują o kształcie dzwona. Wartość @mi decyduje o przesunięciu w poziomie. Jeżeli jest ustawiona na 0, środek wykresu również będzie w punkcie 0 osi X. Zmienna @sigma decyduje o, mówiąc obrazowo, spłaszczeniu całego wykresu. Popatrzmy jeszcze na część danych powstałych w wyniku zapytania (pominąłem wartości krańcowe i zostawiłem środkowe - tam dzieje się najwięcej):

X	Y
-1.000000	0.2420
-0.900000	0.2661
-0.800000	0.2897
-0.700000	0.3123
-0.600000	0.3332
-0.500000	0.3521
-0.400000	0.3683
-0.300000	0.3814
-0.200000	0.3910
-0.100000	0.3970
0.000000	0.3989
0.100000	0.3970
0.200000	0.3910
0.300000	0.3814
0.400000	0.3683
0.500000	0.3521
0.600000	0.3332
0.700000	0.3123
0.800000	0.2897
0.900000	0.2661
1.000000	0.2420

Patrząc na te dane trudno dostrzec znaki szczególne wykresu. Lepiej je widać w Excelu:

Dzwonopodobny wykres funkcji Gaussa z rozkładem standardowym — Wygenerowany przez skrypt SQL wykres funkcji Gaussa.

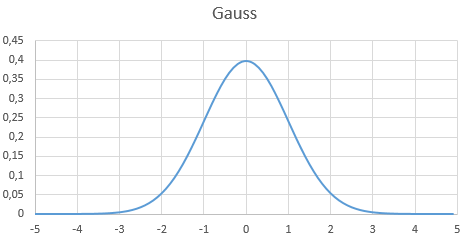
Korzystając z takich danych można już spokojnie generować losowe wartości do testów.

Podsumowanie

Rozkład normalny i może być szeroko wykorzystywany nie tylko do analiz statystycznych, ale także, po odpowiednich przygotowaniach, do testowania bazy danych pod kątem bardziej rzeczywistych danych. Testy na tabelach z mechanicznie generowanymi danymi nie będą tak wartościowe jak testy na danych realnych. Wpis dotyczy rozkładu Gaussa, ale modelowanie statystyczne może iść dużo dalej. W jednym z kolejnych wpisów postaram się pokazać praktyczne zastosowanie nierównomiernego rozkładu do wyświetlania pseudolosowych/sugerowanych artykułów. Teoria teorią, ale praktyka jest najważniejsza.

Kategoria:SQL Server

Paweł Dyl, 2013-12-20

Spis treści:

Rozkład normalny (Gaussa) w SQL Server

Czołówka rozkładów prawdopodobieństwa

Wzór funkcji

Generowanie wartości funkcji w zadanym przedziale

Podsumowanie

Komentarze: