Algorytm Floyda-Warshalla, czyli wyszukiwanie najkrótszej drogi pomiędzy każdą parą wierzchołków
Problem wyszukiwania ścieżek
Wyszukiwanie najkrótszej drogi jest na tyle popularnym problemem w algorytmice, że powstało już wiele rozwiązań. Jednym z tyh algorytmów jest algorytm Floyda-Warshalla, który pozwala na wyszukanie najkrótszej ścieżki pomiędzy wszystkimi wierzchołkami w grafach skierowanych, także w takich, w których poszczególne połączenia są ujeme. Warunek stosowania wag ujemnych jest taki, że nie powstaną ujemne cykle. Istnieją takie sytuacje gdy nie można obliczyć najkrótszej drogi. Może to być spowodowane tym, że nie istnieje połączenie pomiędzy parą wierzchołków, lub w grafie powstały pętle z ujemną wagą. Problem wyszukiwania najkrótszych dróg ma szerokie zastosowanie. Na przykład, możemy poszukiwać najtańszej trasy (koszt jest wagą) z podanego wierzchołka do dowolnego innego w grafie, możemy poszukiwać idealnego miejsca na główną siedzibę firmy, aby odległości pomiędzy siedzibą główną a oddziałami były jak najmniejsze. Możemy zastosować ten algorytm do wyszukiwania połączeń w bazie danych SQL poprzez klucze obce i automatycznie tworzyć złączenia. Można także odwrócić problem i za pomocą tego algorytmu mierzyć przepustowość. W wyniku działania algorytmu otrzymamy takie ścieżki, którymi dotrzemy nie najkócej, ale najszybciej. Zastosowania można mnożyć w nieskończoność, zachęcam do własnej analizy.
Zasada działania algorytmu
Algorytm Floyda-Warshalla przetwarza tzw. macierz wag. Inaczej mówiąc, jest to tablica dwuwymiarowa, w której poszczególne komórki kreślają wagi. Macierz wag, zwana także macierzą optymalnych decyzji, jest macierzą kwadratową. Komórka o indeksie (i,j) określa koszt przejścia z punktu i do punktu j. Co warte przypomnienia, koszt (i,j) nie musi być wcale równy kosztowi (j,i). Co więcej, połączenie może być tylko w jednym kierunku. Te właściwości są charakterystyczne dla grafów skierowanych. Przykład z wyszukiwaniem połączeń w bazie danych SQL mógłby założyć, że połączenia (i,j)=(j,i). Dlaczego? Z prostego powodu. Jeżeli istnieją dwie tabele i jest między nimi jakieś połączenie (klucz obcy), to nie ma znaczenia czy łączymi tabelę A z B, czy B z A.
Ważnym parametrem algorytmu jest zmienna określająca, czy w trakcie obliczeń nie pojawiły się ujemne cykle. Jak taki cykl może wpływać na wartości dróg? Załóżmy, że na swojej drodze napotkaliśmy cykl ujemny. Wyszukując najkrótszą drogę dochodzimy do wniosku, że im więcej razy przejdziemy rozpatrywany cykl (pętlę), tym krótsza będzie droga wynikowa. Jasne jest, że w takiej sytuacji, dążąc do minimalizacji drogi całkowitej, zapętlimy się w nieskończoność. Ta zmienna pozwala zatem określić, czy otrzymane rezultaty są prawidłowe.
W macierzy wejściowej należy wyraźnie rozróżnić wartości określające koszt, od wartości określających brak połączenia. W praktyce stosuje się najczęściej maksymalną lub minimalną wartość z zakresu. Dla naszych celów zdefiniujmy sobie tę wartość jako INF (skrót z języka angielskiego INFinity – nieskończoność). Jeżeli w wynikowej macierzy wag występują jakieś wartości – oznaczają one najkrótszą drogę pomiędzy odpowiednimi węzłami, jeżeli natomiast wartość będzie odpowiadała nieskończoności (INF) to będzie oznaczało, że nie istnieje ścieżka pomiędzy tymi punktami.
Podstawowym elementem algorytmu jest porównanie czy istnieje krótsza droga pomiędzy rozpatrywanymi punktami P1 i P2 przez inny punkt Px. Przykładowo, jeżeli waga pomiędzy P1 i P2 wynosi W12, i istnieje droga z punktu P1 do Px i z punktu Px do P2, i suma tych wag W1x i Wx2 jest mniejsza niż waga W12, wtedy nową wagą z punktu P1 do P2 staje się ta właśnie suma.
Jeżeli Wil+Wlj<Wij to Wij=Wil+Wlj
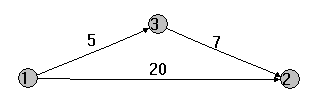
Rys 1. Zasada działania algorytmu Floyda-Warshalla.
Jak można zaobserwować droga bezpośrednia od wierzchołka 1 do 2 jest dłuższa niż droga poprzez wierzchołek 3 (5+7<20). Nową wagą stanie się zatem wartość 12. Takie porównania wykonywane są tyle razy, ile wynosi rozmiar macierzy.
Opcjonalnym parametrem algorytmu jest macierz optymalnych decyzji. Jej istnienie nie wpływa na działanie algorytmu, ale pozwala w dość łatwy sposób na określenie numerów węzłów przez które musimy przejść aby otrzymać podaną wartość drogi. Przechowywanie tego parametru zwiększa prawie dwukrotnie zapotrzebowanie na pamięć algorytmu.
Pseudokod algorytmu
Zmienne i wartości:
i – początek drogi
j – koniec drogi
n – rozmiar macierzy
wij – waga pomiędzy węzłem i a j
INF – nieskończoność
//
for l := 1 to n do
for i := 1 to n do
if wil <> INF then
for j := 1 to n do wij := min(wij, wil + wij)//*
gdzie:
min – minimum; min(a, b) = if a < b then a else b
//*Dla macierzy optymalnych decyzji dodatkowo mamy:
Pij := i jeśli wij <> INF
Pij := 0 jeśli wij = INF
W iteracji, w której wierzchołek l zostaje włączony do drogi, to jest gdy nastąpiła zamiana z drogi bezpośredniej na drogę poprzez wierzchołek dodatkowy podstawiamy pij := plj.
Aby uzyskać wierzchołki będące po drodze pomiędzy dwoma punktami stosujemy odpowiednie wzory.
Złożoność procedury
Analizując algorytm (pseudokod) można łatwo określić zapotrzebowanie na czas obliczeń. W procedurze mamy zagnieżdżenie trzech pętli. Każda z tych pętli działa w zakresie od 1 do n. Widać, że złożoność czasowa wynosi O(n3). Dodatkowo algorytm nie przewiduje żadnych warunków pozwalających na przedwczesne zakończenie algorytmu. Nie ma sensu rozpatrywać złożoności w najlepszym lub najgorszym przypadku. Algorytm ma złożoność O(n3) bez względu na gęstość rozpatrywanej sieci.
W przypadku złożoności pamięciowej sytuacja także jest oczywista. Wyszukująć tylko wartości najkrótszych dróg potrzebujemy NxN słów pamięci (N – rozmiar macierzy) dla zapamiętania macierzy podstawowej. W przypadku gdy chcemy także otrzymać macierz optymalnych decyzji potrzebujemy dodatkowo NxN słów pamięci. Pozostałe zmienne w przypadku dużych wymiarów macierzy nie mają praktycznie żadnego wpływu.
Otrzymujemy złożoności:
Dla macierzy podstawowej – O(n2)
Dla zapamiętania macierzy dróg – O(n2)
W sumie dla całości potrzebujemy 2xNxN słów pamięci.
Ważnym elementem algorytmu jest wyliczanie ścieżki na podstawie wcześniej wyliczonej macierzy optymalnych decyzji. Co jest tutaj istotne? To, że złożoność procedury w najgorszym wypadku wynosi O(n). Algorytm jest liniowy. Co więcej, przeglądane jest tylko tyle wartości, ile jest połączeń na wyszukiwanej ścieżce. Jest to więc znakomity sposób do szukania połączeń w stałych grafach. Jednokrotne przeliczenie może i trwa długo, ale etap właściwy, czyli szukanie ścieżek sprowadza się do prostego przeglądu tablicy optymalnych decyzji.
Określanie drogi na podstawie macierzy optymalnych decyzji
Po zakończeniu działania algorytmu, mając wypełnioną macierz optymalnych decyzji, możemy w prosty sposób otrzymać drogę z dowolnego wierzchołka i do dowolnego wierzchołka j. W celu uzyskania tej drogi można skorzystać ze wzorów:
vq-1 = pivq
vq-2 = pivq-1
...
i = piv1
Przykład:
Mając dany graf:
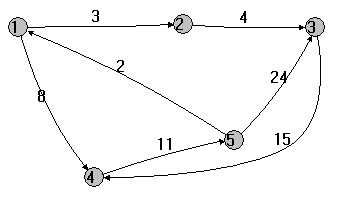
Oraz macierz dla tego grafu:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 3 | 8 | |||
| 2 | 4 | ||||
| 3 | 15 | ||||
| 4 | 11 | ||||
| 5 | 2 | 24 |
I macierz wynikową:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 21 | 3 | 7 | 8 | 19 |
| 2 | 32 | 35 | 4 | 19 | 30 |
| 3 | 28 | 31 | 35 | 15 | 26 |
| 4 | 13 | 16 | 20 | 21 | 11 |
| 5 | 2 | 5 | 9 | 10 | 21 |
Oraz macierz wag:
| 1 | 2 | 3 | 4 | 5 | |
| 1 | 5 | 1 | 2 | 1 | 4 |
| 2 | 5 | 1 | 2 | 3 | 4 |
| 3 | 5 | 1 | 2 | 3 | 4 |
| 4 | 5 | 1 | 2 | 1 | 4 |
| 5 | 5 | 1 | 2 | 1 | 4 |
Spróbujmy otrzymać najkrótszą drogę z węzła 5 do węzła 3.
vq-1=pivq=p52=1
v1=pivq-1=p51=5
(W tym miejscu przerywamy obliczenia)
Zapisujemy rezultaty: 5, 1, 2, 3. Łatwo sprawdzić na grafie, że wynik jest prawidłowy.
Macierz optymalnych decyzji jest tak naprawdę zbiorem punktów poprzedzających ostatni punkt na drodze pomiędzy konkretnymi punktami. W przedstawionym przykładzie ostatnim węzłem na drodze pomiędzy punktami 3 i 5 był punkt 2. Skoro najkrótsza droga z 5 do 3 prowadzi przez 2, to wystarczy teraz odszukać najkrótszą drogę z punktu 5 już nie do punktu 3, ale do punktu 2. Odczytujemy następnie wierzchołek poprzedzający punkt 2 na przeszukiwanej drodze, następnie punkt poprzedzający następnego itd. .Zauważmy, że w przypadku rozpatrywanej macierzy wag, cały czas poruszamy się po tym samym rzędzie, będącym numerem punktu startowego. Spróbujmy zastosować powyższe spostrzeżenia do naszego przykładu. Naszym punktem początkowym jest 5. Przechodzimy więc do piątego rzędu, o pozostałych rzędach zapominamy. Teraz przyglądamy się tylko kolumnom. Zaczynamy od numeru punktu końcowego. Wartością dla tej kolumny jest 2. Zapisujemy tę wartość i przechodzimy do kolumny o tym właśnie numerze. Tam mamy numer 1. Zapisujemy i przechodzimy do kolumny o numerze 1. Tam mamy wartość 5. Algorytm się kończy. W tym momencie mamy zapisane 3(punkt startowy), 2, 1, 5(punkt końcowy). Jak wspomniano macierz optymalnych decyzji jest macierzą poprzedników. Aby zatem otrzymać punkty w poprawnej kolejności wystarczy odwrócić liczby. Otrzymujemy wtedy 5, 1, 2, 3, co jest zgodne z wynikiem.
Uwaga!
Może się zdarzyć, że wartościami w macierzy wag będą umowne wartości nie oznaczające żadnej wartości (powiedzmy INF). Taka sytuacja oznacza, że nie istnieje połączenie pomiędzy odpowiednimi punktami. Aby upewnić się czy istnieje droga wystarczy sprawdzić jedną wartość, bo skoro nie ma poprzednika punktu ostatniego, to nie istnieje żadne połączenie.
Jeżeli ktoś potrzebuje pełnej implementacji, to tutaj można znaleźć kod algorytmu Floyda-Warshalla w C#.NET.
Komentarze:
wij := min(wij, wil + wij)
;)