Rozwiązywanie równań trzeciego stopnia - JavaScript
Zapotrzebowanie obliczeniowe
Rozwiązywanie pewnych grup problemów wymaga zaprzęgnięcia bardziej skomplikowanych wzorów niż te, które są powszechnie znane. O ile z równaniem kwadratowym poradziłaby sobie, tak myślę, większość społeczeństwa, o tyle z równaniem stopnia trzeciego tylko wybrańcy. Większość nie ma potrzeby korzystać z logarytmów, liczb zespolonych i wielomianów - ich potrzeby ograniczają się w najlepszym razie do liczenia procentów i prostych działań typu dodawanie i mnożenie. Wracając do równać trzeciego stopnia - nawet w świecie komputerów są one rzadkością. Nie zmienia to jednak faktu, że pojawić się mogą. Są to problemy optymalizacji procesów opisanych funkcją sześcienną, ale także obliczenia związane z geometrią, między innymi podczas wykrywania przecięć i kolizji krawędzi obiektów, badania krzywych Béziera. Bez względu na potrzebę, zachęcam do zapoznania się z tematem.
Obliczanie pierwiastków równania trzeciego stopnia online
Skoro algorytm napisany jest w JavaScript, można go łatwo przedstawić na stronie. Być może ktoś chce tylko wynik - zainteresowanych szczegółami odsyłam do dalszej części.
Dzięki prostemu formularzowi można przetestować zaprezentowany poniżej kod. Dołożyłem wszelkich starań, aby funkcja właściwie obliczała wszystkie miejsca zerowe. Nigdy nie ma jednak stuprocentowej pewności, czy algorytm będzie działał w każdym możliwym przypadkuPowszechnie znany jest problem zaokrągleń, szczególnie w przypadku takich operacji jak pierwiastkowanie, logarytmowanie, obliczanie wartości funkcji trygonometrycznych. Te drobne, czasami niezauważalne, pojawiające się na dalekim miejscu po przecinku wartości sprawiają, że matematyczne zero nie jest zawsze równe komputerowemu zeru, zamiast matematycznie poprawnej liczbie 2 może wyjść na przykład wartość 2,000000016. Ma to związek z komputerową reprezentacją liczby zdefiniowanej w standardzie IEEE 754 i wartościach pośrednich wykorzystywanych w obliczeniach..
Trochę teorii
Jak zabrać się do obliczania pierwiastków? Najbardziej ogólna postać wielomianu trzeciego stopnia reprezentowana jest następującym wzorem:
ax3 + bx2 + cx + d = 0
To jest nasza postać wyjściowa, ale nie jest ona wygodna. Znacznie wygodniejsza jest postać, która ma współczynnik 1 przy najwyższej potędze. Pokazane poniżej wzory są równoważne: aby otrzymać drugi wzór dzielimy obie strony równania przez współczynnik a:
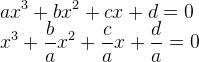
Od teraz zakładamy, że współczynnik a jest równy 1. Kolejnym etapem jest eliminacja elementu z x2. Można to zrobić stosując podstawienie y = x - b/3:
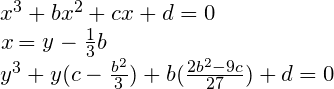
Te złożone współczynniki można sobie zastąpić czymś prostszym, doprowadzając wielomian do bardzo krótkiej postaci:
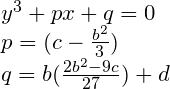
Dalej, podobnie jak w przypadku równania kwadratowego, liczymy wyróżnik. Celowo podałem formy równoważne. To, co jest czytelniejsze matematycznie, nie zawsze jest lepsze dla komputera. Zaraz się wszystko wyjaśni:
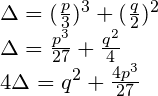
Po tak długich przygotowaniach w końcu można coś policzyć.
Wyróżnik większy od zera
I tak, jeżeli wyróżnik równania jest większy od 0, rozwiązaniem równania jest zawsze wartość:
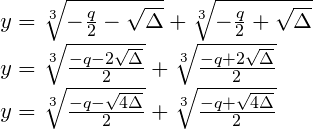
Znów podałem równoważne wzory. Warto zwrócić uwagę na czterokrotność wyróżnika w obu wzorach. Wzór z czterokrotnością wyróżnika pojawia się w algorytmie napisanym w JavaScript, dlatego pozwoliłem sobie wykonać odpowiednie przekształcenia. Dzięki temu nie będzie problemów ze zrozumieniem kodu.
Wyróżnik mniejszy od zera
W takiej postaci pojawia się pewien problem - pierwiastek z liczby ujemnej. Obliczenia wkraczają na obszar liczb zespolonych. To, że podczas obliczeń pojawiają się liczby zespolone nie oznacza, że otrzymamy zespolone rozwiązania - zginą one podczas obliczeń. W celu uproszczenia komputerowych obliczeń wartości zespolone można przedstawić w postaci trygonometrycznej również likwidując zapis z częścią urojoną. Przejdźmy jednak do wzorów - gdy wyróżnik jest mniejszy od zera, równanie ma trzy rozwiązania:
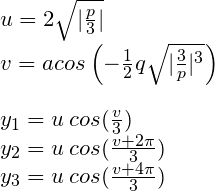
Warto zwrócić uwagę, że współczynnik p będzie tutaj zawsze ujemny. Wyróżnik składa się z sumy kwadratu q (zawsze dodatnie) i trzeciej potęgi p, jasne jest, że p musi być ujemne. Pozwala to zastąpić wartość bezwzględną znakiem minus.
Wyróżnik równy zero
Najtrudniejsze za nami. Sposób na obliczenie pierwiastka przy wyróżniku równym 0 jest znacznie prostszy niż pokazane powyżej. Nie przedłużając, popatrzmy na poniższe wzory:
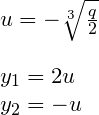
W każdym z przypadków należy pamiętać o tym, że liczymy y. Należy też pamiętać, że y był wyrażony jako x pomniejszone o jedną trzecią współczynnika b. Aby zatem wyliczyć rozwiązania równania pierwotnego należy do otrzymanych y jedną trzecią b dodać. Czy to wszystkie przypadki?
Pozostałe przypadki
Sekcja pozostałych przypadków będzie bardzo prosta dla większości czytelników. To te przypadki, w których współczynnik a jest równy 0. Mamy wtedy do czynienia ze zwykłym równaniem kwadratowym. Nie zamierzam go tutaj przedstawiać, bo jest on powszechnie znany. Strona ma trafiać przede wszystkim do środowiska informatycznego (stąd też mocno skrócona postać wzorów i wyprowadzeń), dlatego najwyższy czas przejść do kodu.
Implementacja w języku JavaScript
Podejrzewam, że większość czytelników przewinęła od razu do tego miejsca. Popatrzmy na kod (HTML +JavaScript) wykorzystany do utworzenia prostego formularza z początku artykułu:
<script> function solveCubicEquation(a, b, c, d) { var zero = 0.0000001, //JavaScript fail to evaluate cube root from negative number - NaN //http://www.ecma-international.org/ecma-262/5.1/#sec-15.8.2.13 cbrt = function (a) { return a >= 0 ? Math.pow(a, 1 / 3) : -Math.pow(-a, 1 / 3); }; if (Math.abs(a) > zero) { // normalize, convert to form: x3 + ax2 + bx + c = 0 b = b / a; c = c / a; d = d / a; var p = c - b * b / 3, q = b * (2 * b * b - 9 * c) / 27 + d, p3 = p * p * p; D = q * q + 4 * p3 / 27, subst = -b / 3; if (D > zero) { D = Math.sqrt(D) var u = cbrt((-q + D) / 2), v = cbrt((-q - D) / 2); return [u + v + subst]; } else if (D < -zero) { //If (D < 0) => p < 0, change sign of p var u = 2 * Math.sqrt(-p / 3), v = Math.acos(-Math.sqrt(-27 / p3) * q / 2) / 3; return [u * Math.cos(v) + subst, u * Math.cos(v + 2 * Math.PI / 3) + subst, u * Math.cos(v + 4 * Math.PI / 3) + subst]; } else { // D zero var u = -cbrt(q / 2); return [2 * u + subst, -u + subst]; } } else { // a = 0, 2nd degree equation: ax3+bx2+cx+d => bx2+cx+d if (Math.abs(b) <= zero) { if (Math.abs(c) <= zero) return []; else return [-d / c]; } var D = c * c - 4 * b * d; if (D > zero) { D = Math.sqrt(D); return [(-c - D) / (2 * b), (-c + D) / (2 * b)]; } else if (D < -zero) { return []; } else { //D = 0 return [-c / (2 * b)]; } } } function solvePolynomialEquation() { var inputs = document.getElementsByClassName('polynomial-equation')[0]; var args = []; for (var i = 0; i < inputs.childNodes.length; i++) if (inputs.childNodes[i].type == 'number') args.push(parseFloat(inputs.childNodes[i].value)); var result = solveCubicEquation.apply(this, args); document.getElementById('polynomial-solution').innerText = result; } </script> <style> .polynomial-equation input{ width:4em; } #polynomial-solution { font-weight:bold;} </style> <div class="polynomial-equation"> <input type="number" value="1" /> x<sup>3</sup> + <input type="number" value="3" /> x<sup>2</sup> + <input type="number" value="0" /> x + <input type="number" value="-4" /> = 0 <input type="button" value="Oblicz" onclick="solvePolynomialEquation();" /> <div>Rozwiązania: <span id="polynomial-solution"></span></div> </div>
Całość można skopiować na pustą stronę HTML i powinno działać. Aplikacja/skrypt nie wymaga żadnych zewnętrznych bibliotek. Warto zwrócić uwagę na nadpisanie wbudowanej funkcji liczącej pierwiastek trzeciego stopnia. Zgodnie ze specyfikacją JavaScript nie da się podnieść liczby ujemnej do skończonej, niecałkowitej potęgi. Pierwiastek trzeciego stopnia to podniesienie liczby do potęgi ⅓. Można przeczytać, że xy powinno, poza innymi przypadkami, zwracać co następuję: jeżeli x < 0 i x jest skończone oraz y nie jest całkowite - NaN. Dobrze wiemy, że da się to jednak wyliczyć, na przykład pierwiastek trzeciego stopnia z -8 to -2 bo -23 to właśnie -8. Pomijając oczywiście pierwiastki zespolone.
Kategoria:JavaScript
Komentarze: