Krzywa Béziera - odległość od punktu i wykrywanie kliknięć
Podstawy matematyczne
Pani na lekcji języka polskiego pyta Jasia: - Jasiu, podaj dwa zaimki osobowe. - Kto? Ja? - Bardzo dobrze szóstka.
Krzywa Béziera to, za różnymi definicjami, parametryczna krzywa powszechnie stosowana w programach inżynierskich CAD, do projektowania grafiki komputerowej, w czcionkach i obiektach SVG. Jest po prostu dobra. Nie oznacza to wcale, że jest łatwa w obsłudze. Rzekłbym, że jest to jedna z bardziej, o ile nie najbardziej skomplikowana figura geometryczna. Linie, wielokąty będące tylko zwielokrotnieniem linii, okręgi, elipsy, prostokąty - wydaje się, że wszystko to jest znacznie prostsze w obsłudze. Pisząc obsłudze mam na myśli podstawowe operacje obliczeniowe typu: wykrywanie krawędzi, przesuwanie, definiowanie kształtu. Te operacje wykonywane są najczęściej za pomocą myszki, a ta, jak wiemy, jest urządzeniem wskazującym. Wskazującym współrzędne X i Y. Problem polega zatem głównie na określeniu, jak te współrzędne X i Y położone są względem krzywej Béziera. Krzywa Béziera w najprostszej postaci ma trzy punkty charakterystyczne - początek, koniec i trzeci, dziwny, bo leżący poza łukiem punkt kontrolny. O tym jednak za chwilę.
Krzywe Béziera to krzywe wielomianowe i mogą, jak to wielomiany, osiągać dowolnie wysoki stopień. Ja postanowiłem zająć się krzywymi drugiego stopnia (zwanymi również kwadratowymi). Takie krzywe zapisuje się w postaci następującego wzoru:
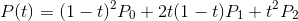
Punkty P0, P1 i P2 to odpowiednio punkt początkowy, kontrolny i środkowy. Zmienna t to parametr... parametrycznej Krzywej Béziera zmieniający się w zakresie [0,1].
Odległość punktu od krzywej Béziera
Punkty krzywej parametrycznej liczone są dla każdej możliwej wartości t z przedziałuW praktyce przedziały mogą być również dyskretyzowane. Podzielenie krzywej na odpowiednią liczbę bardzo krótkich odcinków może sprawiać wrażenie gładkiego łuku.. Dla t=0 będzie to punkt P0, dla t=1 będzie to P2. Każdy punkt pomiędzy końcami ma odpowiadającą mu wartość t. Problem jest ze znalezieniem właściwego t.
Warto wiedzieć, że krzywa Béziera jest różniczkowalna i z tej właściwości skorzystam. Przypomnę, że pochodna jest wektorem (w punkcie t) pokrywającym się ze styczną w punkcie t. Co to daje? Popatrzmy na rysunek:
Wektor styczny jest, podobnie jak krzywa, funkcją t. Przypuśćmy, że obiekt, dla którego szukamy odległości od krzywej, znajduje się w punkcie M. Najkrótsza odległość pomiędzy punktem M i P(t) pojawiłaby się w momencie uzyskania prostopadłości wektora [M, P(t)] z wektorem stycznym. Kiedy takie coś ma miejsce? Ano wtedy, gdy iloczyn skalarny tych wektorów wynosi 0. Popatrzmy zatem na obliczenia. Pochodna w punkcie t będzie wynosiła:
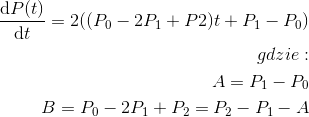
Zamieściłem pod wzorem dwa podstawienia, które będą się pojawiać w obliczeniach i w kodzie. Popatrzmy na sposób obliczenia wektora prostopadłego w punkcie i równanie na prostopadłość tego wektora z wektorem stycznym.
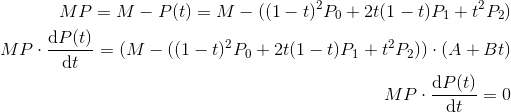
Teraz najłatwiejsza rzecz. Trzeba to wszystko przeliczyć, pomnożyć, przenieść, zredukować i doprowadzić do przejrzystego równania postaci at3+bt2+ct+d. Będzie to równanie trzeciego stopnia, nieco trudniejsze niż te szkolne z deltą. Współczynniki przy kolejnych potęgach t będą (pominę obliczenia) wyglądały następująco:
a=B2 b=3A2 c=2A2+BV d=AV V=P0-M
Wszystkie iloczyny są iloczynami skalarnymi. Sposób dokładnego rozwiązywania równań trzeciego stopnia można znaleźć tutaj: Rozwiązywanie równań trzeciego stopnia - JavaScript. Równanie drugiego stopnia może mieć maksymalnie dwa rozwiązania, równanie trzeciego stopnia ma o jedno więcej - trzy. Nie oznacza to, że trzeba rozpatrywać wszystkie. Przypomnę, że parametryczna krzywa Béziera rysowana jest w zakresie [0,1]. Już samo to pozwoli ograniczyć potencjalne rozwiązania. Gdy więcej niż jedno rozwiązanie mieści się w tym zakresie, a jest taka możliwość, wystarczy dla każdego z tych rozwiązań policzyć odległość pomiędzy punktami P(t) i W. Spośród wyników wybieramy oczywiście ten najmniejszy. Tyle teorii, czas na kod.
Przykład aplikacji obliczającej odległości
Zanim przejdę do części technicznej przyjrzyjmy się aplikacji, którą za chwilę stworzymy. Program na bieżąco wylicza najkrótszą odległość pomiędzy wskaźnikiem myszy a krzywą. Pozwala też na regulację krzywej, to znaczy regulację wszystkich punktów tejże krzywej - początku, końca i punktu kontrolnego. Ruchomy punkt na krzywej wskazuje właśnie to miejsce, do którego jest najbliżej. Uznałem, że warto również narysować punkt, który jest środkiem krzywej Béziera. To punkt liczony dla t=0,5. W niektórych przypadkach łatwiej kontrolować kształtem krzywej przesuwając punkt leżący na tej krzywej niż punkt leżący gdzieś obok. Popatrzmy na rezultat:
Pomocnicze funkcje i obiekty
Aby rozdzielić kod liczenia pierwiastków, obsługi zdarzeń, rysowania i konfigurowania położenia krzywej, postanowiłem wydzielić kilka kluczowych elementów do oddzielnych obiektów. Położyłem większy nacisk na czytelność niż na wydajność. Popatrzmy na ważniejsze funkcje i struktury.
Obiekt reprezentujący punkt i wektor.
Postanowiłem, że punkt i wektor będą reprezentowane przez tę samą strukturę. Punkt jest reprezentowany przez dwie współrzędne, X i Y, które reprezentują jego położenie. Wektor, definiowany jako przesunięcie, również jest reprezentowany przez dwie wartości - tym razem reprezentujące przesunięcie X i Y. Punkt może być wobec tego reprezentowany jako koniec wektora wychodzącego ze środka układu współrzędnych. Popatrzmy na implementacje trzech wykorzystywanych w aplikacji metod:
var vect = function (vx, vy) { var self = this; self.x = vx; self.y = vy; self.sub = function (v) { return new vect(self.x - v.x, self.y - v.y); } self.dot = function (v) { return self.x * v.x + self.y * v.y; } self.contains = function (x, y) { return self.x >= x - 3 && self.x <= x + 3 && self.y >= y - 3 && self.y <= y + 3 } }
Pierwsza metoda to różnica wektorów (punktów). Różnica wektorów jest wektorem, co nie powinno dziwić, różnica punktów, a dokładniej jego współrzędnych, definiuje tenże wektor. Znów dualizm. Druga metoda, dot, oblicza iloczyn skalarny dwóch wektorów (bieżącego i przekazanego w postaci parametru). Iloczyn skalarny jest wyliczany przy współczynnikach równania trzeciego stopnia. Ostatnia funkcja pozwala określić, czy wektor zawiera przekazany w parametrze punkt (x,y) wraz z pewnym otoczeniem. Metoda wykorzystywana jest do konfigurowania punktów krzywej Béziera - należy przecież w jakiś sposób rozpoznać, czy wskaźnik myszki znajduje się nad tymi punktami.
Wartość funkcji Béziera dla parametru
Gdybyśmy zechcieli znaleźć pozycję w układzie współrzędnych dla danej wartości parametru t, moglibyśmy napisać a potem wywołać następującą funkcję:
var bezier = function (t) { var t1 = 1 - t, a = t1 * t1, b = 2 * t * t1, c = t * t; return new vect(a * p0.x + b * p1.x + c * p2.x, a * p0.y + b * p1.y + c * p2.y); }
Funkcja wykorzystywana jest do obliczania pozycji punktu przecięcia stycznej oraz prostej prostopadłej do tej stycznej i przechodzącej przez punkt M. Spośród wszystkich takich punktów wybierany jest ten, który jest najbliżej punktu M.
Pozostałe funkcje
Jest jeszcze kilka innych funkcji przydatnych w aplikacji. Są to między innymi:
- funkcja do liczenia długości wektora (odległości pomiędzy punktami) - liczona jako pierwiastek z sumy kwadratów każdego z wymiarów,
- funkcja do przeliczenia współrzędnych myszki na współrzędne obszaru roboczego - ominięcie niespójności w obsłudze tego atrybutu przez różne przeglądarki,
- funkcja do liczenia miejsc zerowych równania trzeciego stopnia - implementacja i podstawy matematyczne zostały już opisane tutaj: Rozwiązywanie równań trzeciego stopnia - JavaScript.
Wszystkie te funkcje można znaleźć w pełnym listingu umieszczonym na końcu.
Implementacja funkcji liczącej odległość punktu od krzywej Béziera
Po długim wstępie czas na funkcję właściwą. Wbrew pozorom nie będzie ona długa i skomplikowana - wszystko zostało już, chyba wystarczająco, wyjaśnione. Popatrzmy na poniższy listing:
var x = //współrzędna x, y = //współrzędna y, A = p1.sub(p0), B = new vect(p2.x - p1.x - A.x, p2.y - p1.y - A.y), V = new vect(p0.x - x, p0.y - y); ... //rozwiąż równianie trzeciego stopnia var result = solver(B.dot(B), 3 * A.dot(B), 2 * A.dot(A) + B.dot(V), A.dot(V)), //pobierz tylko rozwiązania z zakresu [0,1] valid = result.filter(function (a) { return a >= 0 && a <= 1; }), //zwróć punkt przecięcia p(t) i odległość points = valid.map(function (a) { var v = bezier(a); return { point: v, distance: dist(x - v.x, y - v.y) }; }); //Dodaj punkt początkowy i końcowy - to do nich może być bliżej points.push( { point: p0, distance: dist(x - p0.x, y - p0.y) }, { point: p2, distance: dist(x - p2.x, y - p2.y) }); //znajdź minimalną odległość if (points.length > 0) { var minIndex = 0; for (var i = 1; i < points.length; i++) if (points[i].distance < points[minIndex].distance) minIndex = i; //Pobierz punkt leżący najbliżej var m = points[minIndex]; }
Nazwy punktów, wektorów i współczynników pokrywają się ze wzorami przedstawionymi wcześniej. Funkcja solver to funkcja licząca pierwiastki równania. Dane zwracane są w postaci tablicy o długości od 0 do 3, w zależności od liczby rozwiązań. Ważniejsze miejsca zostały opatrzone komentarzem. W zmiennej m, po przeprowadzeniu wszystkich obliczeń, dostaniemy punkt leżący na krzywej Béziera, do którego mamy najbliżej (licząc od pozycji kursora myszy). Warto zauważyć, że do kolekcji dodawane są punkty końcowe (P0 i P1). Sprawia to, że zawsze otrzymamy jakieś rozwiązanie. Pozostała część aplikacji, dotychczas pominięta, wykonuje zadania poboczne, mające niewiele wspólnego z tematem.
Punkt środkowy krzywej Béziera
Wspomniałem wcześniej, że punkt kontrolny leży całkowicie poza krzywą Béziera. W niektórych przypadkach wygodniej jest jednak posługiwać się punktem środkowym, liczonym dla parametru t=0,5. Dla przeciętnego użytkownika bardziej naturalne wydaje się złapanie krzywej niż jakiegoś pozornie niezależnego punktu. Pomiędzy punktem środkowym a kontrolnym jest dość prosta zależność funkcyjna. Popatrzmy na sposób obliczania punktu środkowego:
var midBezier = function (p0, p1, p2) { var t = 0.5, t1 = 1 - t, a = t1 * t1, b = 2 * t * t1, c = t * t; return new vect(a * p0.x + b * p1.x + c * p2.x, a * p0.y + b * p1.y + c * p2.y); }
Aby uzyskać punkt kontrolny mając dany punkt środkowy wystarczy nieznacznie przekształcić wzór:
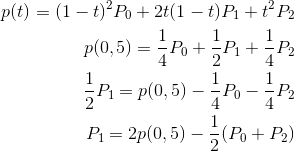
Wartość p(0,5) to właśnie punkt środkowy.
Pełny listing
Na koniec pozwolę sobie umieścić pełny listing aplikacji pokazanej nieco wcześniej:
<html> <head> <title>Odległość punktu od krzywej Béziera</title> </head> <body> <canvas id="canvas" width="400" height="400"></canvas> <script> MouseEvent.prototype.X = function () { if (this.offsetX) return this.offsetX; else return this.layerX - this.currentTarget.offsetLeft; } MouseEvent.prototype.Y = function () { if (this.offsetY) return this.offsetY; else return this.layerY - this.currentTarget.offsetTop; } window.addEventListener("load", function () { var ctx = canvas.getContext("2d"), vect = function (vx, vy) { var self = this; self.x = vx; self.y = vy; self.sub = function (v) { return new vect(self.x - v.x, self.y - v.y); } self.dot = function (v) { return self.x * v.x + self.y * v.y; } self.contains = function (x, y) { return self.x >= x - 3 && self.x <= x + 3 && self.y >= y - 3 && self.y <= y + 3 } }, bezier = function (t) { var t1 = 1 - t, a = t1 * t1, b = 2 * t * t1, c = t * t; return new vect(a * p0.x + b * p1.x + c * p2.x, a * p0.y + b * p1.y + c * p2.y); }, midBezier = function (p0, p1, p2) { var t = 0.5, t1 = 1 - t, a = t1 * t1, b = 2 * t * t1, c = t * t; return new vect(a * p0.x + b * p1.x + c * p2.x, a * p0.y + b * p1.y + c * p2.y); }, p0 = new vect(50, 50), p1 = new vect(350, 200), p2 = new vect(100, 300), solver = function (a, b, c, d) { var zero = 0.0000001, //JavaScript fail to evaluate cube root from negative number - NaN //http://www.ecma-international.org/ecma-262/5.1/#sec-15.8.2.13 cbrt = function (a) { return a >= 0 ? Math.pow(a, 1 / 3) : -Math.pow(-a, 1 / 3); }; if (Math.abs(a) > zero) { // normalize, convert to form: x3 + ax2 + bx + c = 0 b = b / a; c = c / a; d = d / a; var p = c - b * b / 3, q = b * (2 * b * b - 9 * c) / 27 + d, p3 = p * p * p; D = q * q + 4 * p3 / 27, subst = -b / 3; if (D > zero) { D = Math.sqrt(D) var u = cbrt((-q + D) / 2), v = cbrt((-q - D) / 2); return [u + v + subst]; } else if (D < -zero) { //If (D < 0) => p < 0, change sign of p var u = 2 * Math.sqrt(-p / 3), v = Math.acos(-Math.sqrt(-27 / p3) * q / 2) / 3; return [u * Math.cos(v) + subst, u * Math.cos(v + 2 * Math.PI / 3) + subst, u * Math.cos(v + 4 * Math.PI / 3) + subst]; } else { // D zero var u = -cbrt(q / 2); return [2 * u + subst, -u + subst]; } } else { // a = 0, 2nd degree equation: ax3+bx2+cx+d => bx2+cx+d if (Math.abs(b) <= zero) { if (Math.abs(c) <= zero) return []; else return [-d / c]; } var D = c * c - 4 * b * d; if (D > zero) { D = Math.sqrt(D); return [(-c - D) / (2 * b), (-c + D) / (2 * b)]; } else if (D < -zero) { return []; } else { //D = 0 return [-c / (2 * b)]; } } }, dist = function (x, y) { return Math.sqrt(x * x + y * y); }, trim = function (v) { return +v.toFixed(2); }, draw = function (e) { var x = e.X(), y = e.Y(), A = p1.sub(p0), B = new vect(p2.x - p1.x - A.x, p2.y - p1.y - A.y), V = new vect(p0.x - x, p0.y - y), M = midBezier(p0, p1, p2); ctx.fillStyle = "#EEE"; ctx.fillRect(0, 0, 400, 400); ctx.beginPath(); ctx.moveTo(p0.x, p0.y); ctx.quadraticCurveTo(p1.x, p1.y, p2.x, p2.y); ctx.stroke(); ctx.closePath(); ctx.fillStyle = "#00F"; ctx.fillRect(p0.x - 3, p0.y - 3, 6, 6); ctx.fillRect(p1.x - 3, p1.y - 3, 6, 6); ctx.fillRect(p2.x - 3, p2.y - 3, 6, 6); ctx.fillStyle = "#0F0"; ctx.fillRect(M.x - 3, M.y - 3, 6, 6); ctx.fillStyle = "#000"; ctx.fillText("[" + x + ", " + y + "]", 5, 10); var result = solver(B.dot(B), 3 * A.dot(B), 2 * A.dot(A) + B.dot(V), A.dot(V)), valid = result.filter(function (a) { return a >= 0 && a <= 1; }), points = valid.map(function (a) { var v = bezier(a); return { point: v, distance: dist(x - v.x, y - v.y) }; }); points.push( { point: p0, distance: dist(x - p0.x, y - p0.y) }, { point: p2, distance: dist(x - p2.x, y - p2.y) }); if (points.length > 0) { var minIndex = 0; for (var i = 1; i < points.length; i++) if (points[i].distance < points[minIndex].distance) minIndex = i; var m = points[minIndex]; ctx.fillText("min([" + x + ", " + y + "], [" + trim(m.point.x) + ", " + trim(m.point.y) + "]) = " + trim(m.distance), 5, 20); ctx.fillStyle = "#F00"; ctx.fillRect(m.point.x - 3, m.point.y - 3, 6, 6); } }, draggable = [p0, p1, p2], handleMove = function (e) { var x = e.X(), y = e.Y(), hand = false, value; for (var i = 0; i < draggable.length; i++) hand |= draggable[i].contains(x, y); value = hand ? "pointer" : "default"; if (canvas.style.cursor != value) canvas.style.cursor = value; if (mouse.dragged) { var dx = x - mouse.x, dy = y - mouse.y; mouse.x = x; mouse.y = y; mouse.dragged.x += dx; mouse.dragged.y += dy; } }, mouse = { dragged: null, x: 0, y: 0 }, checkDragStart = function (e) { var x = e.X(), y = e.Y(); for (var i = 0; i < draggable.length; i++) if (draggable[i].contains(x, y)) { mouse.dragged = draggable[i]; mouse.x = x; mouse.y = y; } }, stopDrag = function (e) { mouse.dragged = null; }; draw({ X: function () { return 0; }, Y: function () { return 0; } }); canvas.addEventListener("mouseout", stopDrag); canvas.addEventListener("mouseup", stopDrag); canvas.addEventListener("mousedown", checkDragStart); canvas.addEventListener("mousemove", function (e) { handleMove(e); draw(e); }); }); </script> </body> </html>
Kategoria:JavaScript
Brak komentarzy - bądź pierwszy